Rest in Peace, Dr./Professor Harry Markowitz, who passed last week at age 95. The picture shows him accepting the Nobel in Economics in 1990. Markowitz is known as the father of “Modern Portfolio Theory”, which for all practical purposes, told us that you should diversify your portfolio.
Of course, it wasn’t like investors didn’t know this, with maxims like “Don’t put all your eggs in the same basket”. But as our friend, Corey Hoffstein from Newfound Research put it, Markovitz quantified diversification, which was a huge leap forward for constructing portfolios.
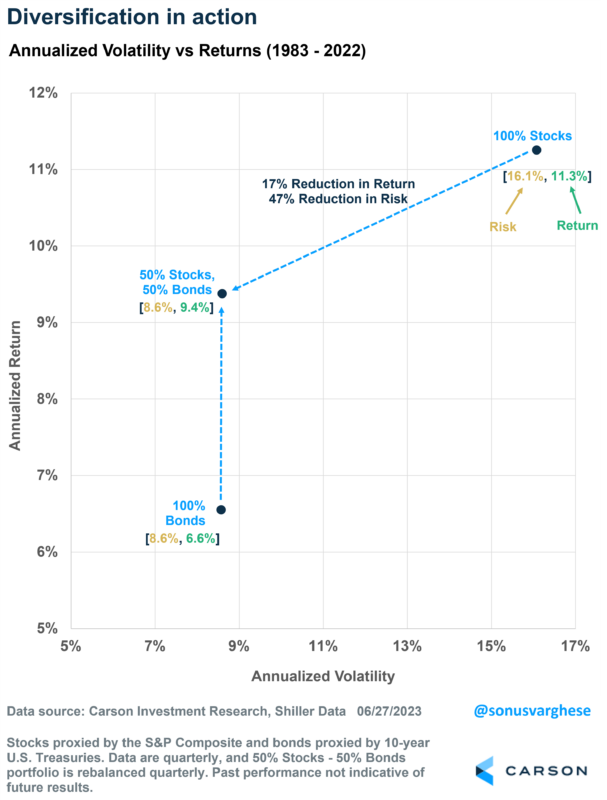
On the surface, it may seem like all of us want to get the highest return for our investments – which would lead us to put all our money on the investment with the highest return. For example, over the past 40 years (1983 – 2022), stocks have gained 11.3% per year*, while 10-year US Treasuries have gained 6.6%.
So, case closed? Put 100% in stocks?

Stay on Top of Market Trends
The Carson Investment Research newsletter offers up-to-date market news, analysis and insights. Subscribe today!
"*" indicates required fields
Not quite, because there is a matter of risk and how much we are willing/able to accept. In fact, the last 40 years have seen four massive bear markets (1987, 2000-2003, 2007-2009, and 2020). So, we may want to be aware of how much risk we want to take, and this is where Markowitz’s work comes in.
He showed that you can construct a portfolio of different assets with a similar return but lower level of risk.
In other words, for a given level of risk, you can create a portfolio that maximizes return. Conversely, for a given level of return, you can construct a portfolio that minimizes risk.
This risk-return framework is widely used for portfolio construction, and we can thank Markowitz for that.
Diversification in action
Between 1983 and 2022, stocks gained 11.3% per year. But “risk” was about 16%, as measured by annualized volatility (standard deviation). Meanwhile, bonds (10-year US treasuries) gained 6.6% per year, with an annualized volatility of 8.6%.
Now here’s something interesting: a portfolio made up of half stocks and half bonds would have gained 9.4% per year, with almost the same level of risk as a 100% bond portfolio!
Relative to a 100% stock portfolio, the 50-50 portfolio saw its risk reduced by almost half, while giving up less than a fifth of the return.
In fact, one thing you may be wondering is: shouldn’t a 50-50 portfolio have a volatility that is average of stocks and bonds, i.e. about 12%?
Yes, that would be the case if stocks and treasuries were perfectly correlated with each other. But they’re not. In fact, over the 40-year period, the correlation was -13%.
Which means when stocks zigged, more often than not bonds zagged. And vice versa.
The negative correlation pulled down the volatility even more than you’d expect if you simply averaged the volatility of stocks and bonds. That’s diversification for you, and a key insight from Markowitz’s work.
Correlation is key
A lot of people ask me: what’s the one metric you look at when you consider including a new investment in a portfolio?
It’s hard to pick any single metric, and we don’t. But if I absolutely had to, I’d pick correlation. Here at the Carson Investment Research team, we think about it in terms of something called the “Marginal Sharpe Ratio”.
The Sharpe Ratio is essentially the amount of excess return you expect from an investment over a risk-free asset like cash, per unit of risk (volatility). Say, an asset has an expected return of 11% with volatility of 16%. Assuming cash pays 3%, the Sharpe ratio is calculated as 0.5, = (11-3)/16.
Usually, we’re always looking to maximize the return for a portfolio given a level of risk we’re comfortable with, i.e., maximize its Sharpe ratio.
The Sharpe ratio is useful for comparing one investment to another. But by itself, it misses correlation and the impact of including a new investment in a portfolio.
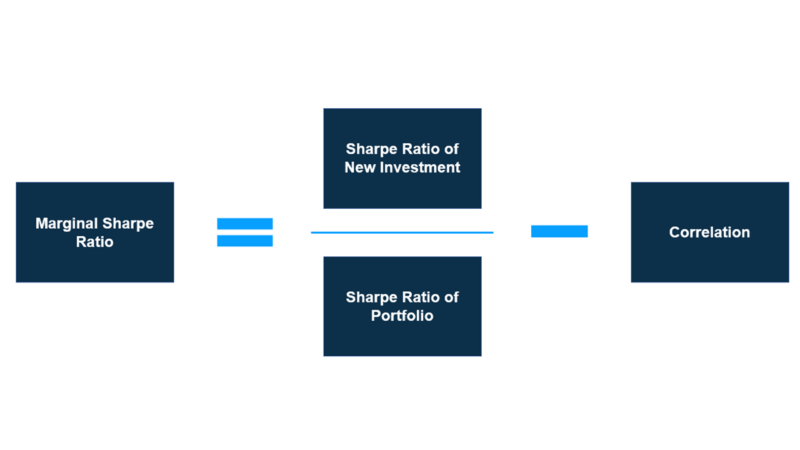
That’s where the Marginal Sharpe Ratio is useful. This metric measures the amount by which a portfolio’s Sharpe ratio will increase (or decrease) when you include a new investment in it. It’s calculated as:
Correlation in this case is the correlation of the new investment with the current portfolio.
Typically, you include a new investment in a portfolio only if its Marginal Sharpe Ratio is above zero. This leads to an interesting place, with some mathematical manipulation. You include the new investment in your portfolio only if,
Here’s an example of how this is quite powerful. Say an existing portfolio had a Sharpe ratio of 0.5, and you’re considering including an investment that has a Sharpe of just 0.20. Normally, you’d say, “forget it”. But let’s say it had a -0.1 correlation with the current portfolio. In which case,
0.25 is greater than -0.1 x 0.5 (= -0.05)
The Marginal Sharpe Ratio of the new investment works out to be 0.5.
In short, the portfolio would benefit by including the new investment in it.
Obviously, there are other considerations too, and these should not be the only metrics you look at when considering new investments. And this is not to say that you should only consider investments with negative correlations to your existing portfolio. But negative and low correlations help, a lot.
Correlation is as important as return and risk when considering new investments for inclusion into a portfolio.
Here at the Carson Investment Research Team, diversification is part of our core philosophy and correlations are an integral part of our portfolio construction process.
And we are extremely grateful to Harry Markowitz for that.
1815353-0623-A